Trang này được dịch bởi Cloud Translation API.

Chuyển đổi WebGL

Gregg Tavares

Dịch 2D WebGL

Trước khi chuyển sang 3D, hãy cùng tìm hiểu thêm một chút về 2D. Vui lòng đợi một lát. Bài viết này có vẻ quá rõ ràng đối với một số người, nhưng tôi sẽ trình bày chi tiết hơn trong một vài bài viết.

Bài viết này là phần tiếp theo của loạt bài viết bắt đầu bằng phần Kiến thức cơ bản về WebGL. Nếu chưa đọc, bạn nên đọc ít nhất là chương đầu tiên rồi quay lại đây. Translation (bản dịch) là một số tên toán học phức tạp, về cơ bản có nghĩa là "chuyển" một cái gì đó. Tôi cho rằng việc di chuyển một câu từ tiếng Anh sang tiếng Nhật cũng phù hợp, nhưng trong trường hợp này, chúng ta đang nói về việc di chuyển hình học. Bằng cách sử dụng mã mẫu mà chúng ta đã kết thúc trong bài đăng đầu tiên, bạn có thể dễ dàng dịch hình chữ nhật chỉ bằng cách thay đổi các giá trị được truyền đến setRectangle phải không? Dưới đây là một mẫu dựa trên mẫu trước đó.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

Mọi thứ vẫn ổn. Nhưng giờ hãy tưởng tượng chúng ta muốn làm tương tự với một hình dạng phức tạp hơn. Giả sử chúng ta muốn vẽ chữ "F" gồm 6 hình tam giác như sau.

Dưới đây là mã hiện tại, chúng ta sẽ phải thay đổi setRectangle thành một mã tương tự như sau.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

Bạn có thể thấy rằng cách này sẽ không mở rộng quy mô tốt. Nếu muốn vẽ một số hình học rất phức tạp với hàng trăm hoặc hàng nghìn dòng, chúng ta sẽ phải viết một số mã khá phức tạp. Ngoài ra, mỗi khi chúng ta vẽ, JavaScript phải cập nhật tất cả các điểm. Có một cách đơn giản hơn. Bạn chỉ cần tải hình học lên và dịch trong chương trình đổ bóng. Dưới đây là chương trình đổ bóng mới

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

và chúng ta sẽ điều chỉnh cấu trúc mã một chút. Đối với một, chúng ta chỉ cần thiết lập hình học một lần.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

Sau đó, chúng ta chỉ cần cập nhật u_translation trước khi vẽ bằng bản dịch mà chúng ta mong muốn.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Lưu ý setGeometry chỉ được gọi một lần. Nó không còn nằm bên trong drawScene nữa.

Giờ đây, khi chúng ta vẽ, WebGL thực sự đang làm mọi thứ. Tất cả những gì chúng ta đang làm là thiết lập một bản dịch và yêu cầu bản dịch đó vẽ. Ngay cả khi hình học của chúng ta có hàng chục nghìn điểm, mã chính vẫn sẽ giữ nguyên.

Xoay 2D WebGL

Tôi phải thú nhận ngay từ đầu rằng tôi không biết cách giải thích này có hợp lý hay không, nhưng thôi cứ thử xem sao.

Trước tiên, tôi muốn giới thiệu cho bạn về "vòng tròn đơn vị". Nếu bạn còn nhớ bài toán cấp hai (đừng ngủ gật nhé!), thì một vòng tròn có bán kính. Bán kính của một hình tròn là khoảng cách từ tâm của hình tròn đến cạnh. Vòng tròn đơn vị là một vòng tròn có bán kính 1.

Nếu bạn còn nhớ kiến thức toán học cơ bản lớp 3, thì khi bạn nhân một số với 1, số đó sẽ không thay đổi. Do đó, 123 * 1 = 123. Khá cơ bản phải không? Vâng, một vòng tròn đơn vị, một vòng tròn có bán kính 1.0 cũng là một dạng của 1. Đó là một số 1 xoay. Vì vậy, bạn có thể nhân một số với vòng tròn đơn vị này và theo một cách nào đó, nó giống như việc nhân với 1, ngoại trừ việc phép thuật xảy ra và mọi thứ xoay vòng. Chúng ta sẽ lấy giá trị X và Y đó từ bất kỳ điểm nào trên vòng tròn đơn vị và nhân hình học của chúng ta với các giá trị đó từ mẫu trước đó. Sau đây là nội dung cập nhật cho chương trình đổ bóng.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

Và chúng ta cập nhật JavaScript để có thể truyền 2 giá trị đó vào.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Tại sao phương pháp này hiệu quả? Hãy xem xét toán học.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

Giả sử bạn có một hình chữ nhật và muốn xoay hình chữ nhật đó. Trước khi bạn bắt đầu xoay, góc trên cùng bên phải sẽ ở vị trí 3.0, 9.0. Hãy chọn một điểm trên vòng tròn đơn vị 30 độ theo chiều kim đồng hồ từ 12 giờ.

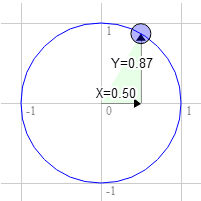
Vị trí trên vòng tròn là 0,50 và 0,87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

Đó chính là nơi chúng ta cần

Tương tự đối với 60 độ theo chiều kim đồng hồ

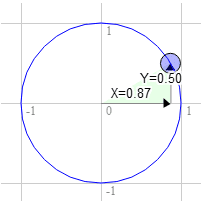
Vị trí trên vòng tròn là 0,87 và 0,50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

Bạn có thể thấy rằng khi chúng ta xoay điểm đó theo chiều kim đồng hồ sang phải, giá trị X sẽ lớn hơn và giá trị Y sẽ nhỏ hơn. Nếu tiếp tục vượt quá 90 độ, X sẽ bắt đầu nhỏ lại và Y sẽ bắt đầu lớn hơn. Mẫu đó giúp chúng ta xoay. Các điểm trên vòng tròn đơn vị còn có một tên khác. Chúng được gọi là sin và cos. Vì vậy, đối với bất kỳ góc nào, chúng ta chỉ cần tra cứu sin và cos như sau.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

Nếu sao chép và dán mã vào bảng điều khiển JavaScript rồi nhập printSineAndCosignForAngle(30), bạn sẽ thấy mã này in ra s = 0.49 c= 0.87 (lưu ý: tôi làm tròn các số). Nếu kết hợp tất cả các thành phần này, bạn có thể xoay hình học theo bất kỳ góc nào bạn muốn. Bạn chỉ cần đặt độ xoay thành sin và cosin của góc mà bạn muốn xoay đến.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

Tôi hy vọng bạn hiểu được. Tiếp theo là một ví dụ đơn giản hơn. Tỷ lệ.

Radian là gì?

Radian là một đơn vị đo lường được dùng với vòng tròn, vòng quay và góc. Tương tự như việc đo khoảng cách theo inch, yard, mét, v.v., chúng ta có thể đo góc theo độ hoặc rađian.

Có thể bạn đã biết rằng toán học với đơn vị đo lường theo hệ mét dễ hơn toán học với đơn vị đo lường theo hệ đo lường Anh. Để chuyển từ inch sang feet, chúng ta chia cho 12. Để chuyển từ inch sang yard, chúng ta chia cho 36. Tôi không biết bạn thế nào, chứ tôi không thể chia cho 36 trong đầu. Với chỉ số, việc này sẽ dễ dàng hơn nhiều. Để chuyển từ milimét sang centimet, chúng ta chia cho 10. Để chuyển từ milimét sang mét, chúng ta chia cho 1000. Tôi có thể chia cho 1000 trong đầu.

Radian và độ tương tự nhau. Độ làm cho toán học trở nên khó khăn. Radian giúp việc tính toán trở nên dễ dàng. Một vòng tròn có 360 độ nhưng chỉ có 2π radian. Vì vậy, một vòng quay đầy đủ là 2π radian. Một nửa vòng quay là π radian. 1/4 vòng, tức là 90 độ là π/2 radian. Vì vậy, nếu bạn muốn xoay một nội dung 90 độ, chỉ cần sử dụng Math.PI * 0.5. Nếu bạn muốn xoay 45 độ, hãy sử dụng Math.PI * 0.25, v.v.

Hầu hết các phép toán liên quan đến góc, vòng tròn hoặc độ xoay đều hoạt động rất đơn giản nếu bạn bắt đầu suy nghĩ theo radian. Vì vậy, hãy thử. Sử dụng radian, không phải độ, ngoại trừ trong màn hình giao diện người dùng.

Tỷ lệ 2D WebGL

Việc mở rộng quy mô cũng dễ dàng như việc dịch.

Chúng ta nhân vị trí với tỷ lệ mong muốn. Sau đây là những thay đổi so với mẫu trước.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

và thêm JavaScript cần thiết để đặt tỷ lệ khi vẽ.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Một điều cần lưu ý là việc điều chỉnh theo tỷ lệ bằng một giá trị âm sẽ đảo ngược hình học của chúng ta. Tôi hy vọng 3 chương cuối này đã giúp bạn hiểu rõ về việc dịch chuyển, xoay và điều chỉnh tỷ lệ. Tiếp theo, chúng ta sẽ tìm hiểu về ma trận kết hợp cả 3 loại ma trận này thành một dạng đơn giản hơn và thường hữu ích hơn.

Tại sao là "F"?

Lần đầu tiên tôi thấy người dùng sử dụng chữ "F" là trên một hoạ tiết. Bản thân chữ "F" không quan trọng. Điều quan trọng là bạn có thể xác định hướng của hình ảnh từ mọi hướng. Ví dụ: nếu sử dụng biểu tượng trái tim ♥ hoặc tam giác △, chúng ta không thể biết liệu biểu tượng đó có bị lật theo chiều ngang hay không. Một vòng tròn ○ sẽ còn tệ hơn. Có thể nói, một hình chữ nhật có màu sẽ hoạt động với nhiều màu sắc ở mỗi góc, nhưng sau đó bạn sẽ phải nhớ góc nào là góc nào. Bạn có thể nhận ra hướng của chữ F ngay lập tức.

Bất kỳ hình dạng nào mà bạn có thể xác định hướng sẽ hoạt động, tôi chỉ sử dụng "F" kể từ khi tôi được "F"irst giới thiệu về ý tưởng này.

Ma trận 2D WebGL

Trong 3 chương vừa qua, chúng ta đã tìm hiểu cách dịch hình học, xoay hình học và điều chỉnh tỷ lệ hình học. Dịch, xoay và chuyển tỷ lệ được xem là một loại "biến đổi". Mỗi phép biến đổi này đều yêu cầu thay đổi đối với chương trình đổ bóng và mỗi phép biến đổi trong số 3 phép biến đổi này đều phụ thuộc vào thứ tự.

Ví dụ: đây là tỷ lệ 2, 1, độ xoay 30% và dịch chuyển 100, 0.

Và đây là thông tin dịch chuyển 100,0, xoay 30% và tỷ lệ 2, 1

Kết quả hoàn toàn khác nhau. Tệ hơn nữa, nếu cần ví dụ thứ hai, chúng ta sẽ phải viết một chương trình đổ bóng khác áp dụng phép dịch, xoay và tỷ lệ theo thứ tự mới mong muốn. Vâng, một số người thông minh hơn tôi nhiều đã nhận ra rằng bạn có thể làm tất cả những việc tương tự bằng toán học ma trận. Đối với 2D, chúng ta sử dụng ma trận 3x3. Ma trận 3x3 giống như lưới có 9 ô.

1.0	2	3
4	5	6.0
7.0	8.0	9.0

Để tính toán, chúng ta nhân vị trí xuống các cột của ma trận rồi cộng các kết quả lại với nhau. Vị trí của chúng ta chỉ có 2 giá trị là x và y, nhưng để thực hiện phép tính này, chúng ta cần 3 giá trị, vì vậy, chúng ta sẽ sử dụng 1 cho giá trị thứ ba. Trong trường hợp này, kết quả của chúng ta sẽ là

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

Bạn có thể đang nhìn vào đó và nghĩ "ĐIỂM CỦA VIỆC NÀY LÀ GÌ". Giả sử chúng ta có một bản dịch. Chúng ta sẽ gọi số lượng bản dịch mà chúng ta muốn dịch là tx và ty. Hãy tạo một ma trận như sau

1.0	0,0	0,0
0,0	1.0	0,0
tx	ty	1.0

Và giờ hãy xem

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

Nếu bạn còn nhớ đại số, chúng ta có thể xoá mọi vị trí nhân với 0. Việc nhân với 1 không có tác dụng gì nên hãy đơn giản hoá để xem điều gì đang xảy ra

newX = x + tx;
newY = y + ty;

Và những thông tin khác chúng ta không thực sự quan tâm. Mã này trông giống như mã dịch trong ví dụ về bản dịch của chúng ta. Tương tự, hãy thực hiện thao tác xoay. Như đã chỉ ra trong bài viết về việc xoay, chúng ta chỉ cần sin và cos của góc mà chúng ta muốn xoay.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

Và chúng ta xây dựng một ma trận như sau

c	-s	0,0
s	c	0,0
0,0	0,0	1.0

Áp dụng ma trận, chúng ta sẽ có kết quả như sau

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

Chúng ta sẽ được kết quả sau khi bôi đen tất cả các phép nhân với 0 và 1

newX = x *  c + y * s;
newY = x * -s + y * c;

Đây chính xác là những gì chúng ta có trong mẫu xoay. Và cuối cùng là quy mô. Chúng ta sẽ gọi 2 hệ số tỷ lệ là sx và sy. Chúng ta sẽ tạo một ma trận như sau

sx	0,0	0,0
0,0	sy	0,0
0,0	0,0	1.0

Áp dụng ma trận, chúng ta sẽ có kết quả như sau

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

điều này thực sự

newX = x * sx;
newY = y * sy;

Tương tự như mẫu tỷ lệ của chúng ta. Tôi chắc chắn rằng bạn vẫn còn đang suy nghĩ. Vậy thì sao? Mục đích là gì. Có vẻ như chúng ta phải làm nhiều việc chỉ để làm cùng một việc mà chúng ta đã làm? Đây là lúc điều kỳ diệu xảy ra. Hóa ra chúng ta có thể nhân các ma trận với nhau và áp dụng tất cả các phép biến đổi cùng một lúc. Giả sử chúng ta có hàm matrixMultiply, hàm này lấy hai ma trận, nhân các ma trận đó rồi trả về kết quả. Để làm rõ hơn, hãy tạo các hàm để tạo ma trận cho phép dịch, xoay và chia tỷ lệ.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

Bây giờ, hãy thay đổi chương trình đổ bóng. Chương trình đổ bóng cũ có dạng như sau

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

Chương trình đổ bóng mới của chúng ta sẽ đơn giản hơn nhiều.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

Và sau đây là cách chúng tôi sử dụng

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

Tuy nhiên, bạn có thể thắc mắc: điều này có ý nghĩa gì? Điều đó có vẻ không mang lại nhiều lợi ích . Tuy nhiên, giờ đây, nếu muốn thay đổi thứ tự, chúng ta không cần phải viết chương trình đổ bóng mới. Chúng ta chỉ cần thay đổi phép tính.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

Việc có thể áp dụng các ma trận như thế này đặc biệt quan trọng đối với ảnh động phân cấp như cánh tay trên cơ thể, mặt trăng trên hành tinh xung quanh mặt trời hoặc cành trên cây. Để biết ví dụ đơn giản về ảnh động phân cấp, hãy vẽ "F" 5 lần, nhưng mỗi lần hãy bắt đầu bằng ma trận từ "F" trước đó.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

Để thực hiện việc này, chúng ta đã giới thiệu hàm makeIdentity tạo một ma trận nhận dạng. Ma trận nhận dạng là một ma trận thể hiện hiệu quả 1.0, vì vậy nếu bạn nhân với ma trận nhận dạng thì sẽ không có gì xảy ra. Cũng giống như

X * 1 = X

cũng vậy

matrixX * identity = matrixX

Dưới đây là mã để tạo một ma trận nhận dạng.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

Một ví dụ khác: Trong mọi mẫu cho đến nay, chữ "F" của chúng ta xoay quanh góc trên cùng bên trái. Điều này là do toán học mà chúng ta đang sử dụng luôn xoay quanh gốc và góc trên cùng bên trái của "F" nằm ở gốc, (0, 0) Nhưng giờ đây, vì chúng ta có thể thực hiện toán học ma trận và chúng ta có thể chọn thứ tự áp dụng phép biến đổi, nên chúng ta có thể di chuyển gốc trước khi áp dụng các phép biến đổi còn lại.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

Khi sử dụng kỹ thuật đó, bạn có thể xoay hoặc điều chỉnh tỷ lệ từ bất kỳ điểm nào. Giờ bạn đã biết cách Photoshop hoặc Flash cho phép bạn di chuyển điểm xoay. Hãy cùng điên rồ hơn nữa. Nếu quay lại bài viết đầu tiên về kiến thức cơ bản về WebGL, bạn có thể nhớ rằng chúng ta có mã trong chương trình đổ bóng để chuyển đổi từ pixel sang không gian cắt như sau.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

Nếu bạn xem lần lượt từng bước đó, bước đầu tiên, "chuyển đổi từ pixel thành 0,0 đến 1,0", thực sự là một phép tính theo tỷ lệ. Thao tác thứ hai cũng là một phép tính theo tỷ lệ. Tiếp theo là phép dịch và phép cuối cùng sẽ chia tỷ lệ Y cho -1. Chúng ta thực sự có thể làm tất cả những việc đó trong ma trận mà chúng ta truyền vào chương trình đổ bóng. Chúng ta có thể tạo 2 ma trận tỷ lệ, một ma trận để tỷ lệ theo 1.0/độ phân giải, một ma trận khác để tỷ lệ theo 2.0, một ma trận thứ ba để dịch theo -1.0, -1.0 và một ma trận thứ tư để tỷ lệ Y theo -1, sau đó nhân tất cả các ma trận này với nhau. Tuy nhiên, vì toán học đơn giản, chúng ta sẽ chỉ tạo một hàm tạo trực tiếp ma trận "mặt chiếu" cho một độ phân giải nhất định.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

Giờ đây, chúng ta có thể đơn giản hoá chương trình đổ bóng hơn nữa. Dưới đây là toàn bộ chương trình đổ bóng đỉnh mới.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

Và trong JavaScript, chúng ta cần nhân với ma trận chiếu

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

Chúng tôi cũng xoá mã đặt độ phân giải. Với bước cuối cùng này, chúng ta đã chuyển từ một chương trình đổ bóng khá phức tạp với 6-7 bước thành một chương trình đổ bóng rất đơn giản chỉ với 1 bước nhờ phép toán ma trận kỳ diệu.

Tôi hy vọng bài viết này đã giúp bạn hiểu rõ hơn về toán học ma trận. Tiếp theo, tôi sẽ chuyển sang 3D. Trong ma trận 3D, toán học tuân theo các nguyên tắc và cách sử dụng tương tự. Tôi bắt đầu với 2D để hy vọng mọi người có thể dễ hiểu.