عمليات تحويل WebGL

Gregg Tavares

الترجمة ثنائية الأبعاد باستخدام WebGL

قبل الانتقال إلى الصور الثلاثية الأبعاد، لنركّز على الصور ثنائية الأبعاد لبعض الوقت. يُرجى الانتظار. قد تبدو هذه المقالة واضحة جدًا لبعض المستخدمين، ولكن سأوضّح بعض النقاط في بضع مقالات.

هذه المقالة هي تتمة لسلسلة تبدأ بـ أساسيات WebGL. إذا لم يسبق لك قراءة هذا القسم، نقترح عليك قراءة الفصل الأول على الأقل ثم الرجوع إلى هنا. الترجمة هي اسم رياضيات غريب يعني في الأساس "نقل" شيء ما. أعتقد أنّ نقل جملة من الإنجليزية إلى اليابانية مناسب أيضًا، ولكن في هذه الحالة نتحدث عن نقل الأشكال الهندسية. باستخدام نموذج الرمز البرمجي الذي توصلنا إليه في المشاركة الأولى، يمكنك بسهولة ترجمة المستطيل من خلال تغيير القيم التي تم تمريرها إلى setRectangle، أليس كذلك؟ في ما يلي عيّنة استنادًا إلى عيّنة سابقة.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

كل شيء على ما يرام حتى الآن. لنفترض الآن أنّنا نريد إجراء الشيء نفسه باستخدام شكل أكثر تعقيدًا. لنفترض أنّنا أردنا رسم حرف "F" يتألّف من 6 مثلثات على النحو التالي.

في ما يلي الرمز البرمجي الحالي الذي يجب تغيير setRectangle فيه إلى شيء أشبه بهذا.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

نأمل أن تكون قد لاحظت أنّ هذا الإجراء لن يؤدي إلى توسيع نطاق الوصول إلى الجمهور بشكلٍ جيد. إذا أردنا رسم بعض الأشكال الهندسية المعقّدة للغاية التي تتضمّن مئات أو آلاف الأسطر، علينا كتابة بعض الرموز البرمجية المعقّدة. بالإضافة إلى ذلك، في كل مرة نرسم فيها JavaScript، يجب تعديل جميع النقاط. هناك طريقة أبسط. ما عليك سوى تحميل الشكل الهندسي وإجراء الترجمة في برنامج Shader. إليك المخطّط اللوني الجديد

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

وسنعيد صياغة الرمز البرمجي قليلاً. على سبيل المثال، نحتاج إلى ضبط الشكل الهندسي مرة واحدة فقط.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

بعد ذلك، ما عليك سوى تعديل u_translation قبل أن نرسم الترجمة التي نريدها.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

يتمّ استدعاء الإشعار setGeometry مرّة واحدة فقط. لم يعُد داخل drawScene.

الآن، عندما نرسم، تُجري WebGL كل شيء تقريبًا. ما عليك سوى ضبط ترجمة وطلب الرسم. وحتى إذا كانت الأشكال الهندسية تتضمّن عشرات الآلاف من النقاط، سيظل الرمز الرئيسي كما هو.

دوران ثنائي الأبعاد باستخدام WebGL

سأقرّ على الفور بأنّني لا أعلم ما إذا كانت الطريقة التي أشرح بها هذا الأمر منطقية، ولكن سأحاول ذلك على أي حال.

أولاً، أريد أن أقدّم لك ما يُعرف باسم "دائرة الوحدة". إذا كنت تتذكر دروس الرياضيات في المرحلة الإعدادية (لا تنام الآن)، يكون للدائرة نصف قطر. نصف قطر الدائرة هو المسافة من مركز الدائرة إلى الحافة. الدائرة الوحدة هي دائرة نصف قطرها 1.0.

إذا كنت تتذكر من الرياضيات الأساسية في الصف الثالث، إذا كنت تضرب أيّ عدد بـ 1، سيظلّ كما هو. وبالتالي، 123 * 1 = 123. خطوات بسيطة، أليس كذلك؟ حسنًا، دائرة الوحدة، وهي دائرة نصف قطرها 1.0، هي أيضًا شكل من أشكال العدد 1. وهي رقم 1 متغيّر. وبالتالي، يمكنك ضرب أيّ عدد في دائرة الوحدة هذه، ويشبه ذلك ضربه في 1، إلا أنّه يحدث سحر وتدور الأشياء. سنأخذ قيمة X وY من أي نقطة على الدائرة الوحدة وسنضرب الشكل الهندسي بها من عيّنتنا السابقة. في ما يلي التعديلات التي أجريناها على برنامج تشويش الصورة.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

ونعدّل JavaScript لنتمكّن من تمرير هاتين القيمتَين.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

ما هي أهمية ذلك؟ حسنًا، لنلقِ نظرة على العمليات الحسابية.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

لنفترض أنّ لديك مستطيلاً وتريد تدويره. قبل بدء عملية الدوران، تكون القيمة في أعلى يسار الشاشة 3.0 و9.0. لنختار نقطة على الدائرة الوحدة بزاوية 30 درجة باتجاه عقارب الساعة من الساعة 12.

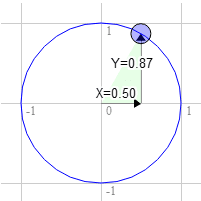
الموقف على الدائرة هو 0.50 و0.87

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

هذا هو المكان الذي نحتاجه بالضبط

وينطبق الأمر نفسه على 60 درجة في اتجاه عقارب الساعة.

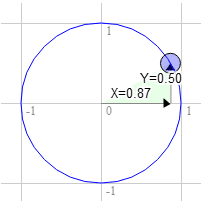
الموضع على الدائرة هو 0.87 و0.50

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

يمكنك ملاحظة أنّه عند تدوير هذه النقطة باتجاه عقارب الساعة إلى اليمين، تزداد قيمة X وتقلّ قيمة Y. إذا استمرّت الزاوية في الزيادة إلى أكثر من 90 درجة، سيبدأ X في الانخفاض مرة أخرى وسيبدأ Y في الزيادة. يمنحنا هذا النمط دورانًا. هناك اسم آخر للنقاط على دائرة الوحدة. يُطلق عليهما جيب الزاوية وجيب التمام. وبالتالي، بالنسبة إلى أي زاوية معيّنة، يمكننا البحث عن جيب الزاوية وجيب التمام على النحو التالي.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

إذا نسخت الرمز والصقته في وحدة تحكّم JavaScript وكتبت printSineAndCosignForAngle(30)، سترى أنّه يطبع s = 0.49 c= 0.87 (ملاحظة: لقد تم تقريب الأرقام). إذا جمعت كل هذه العناصر معًا، يمكنك تدوير الشكل الهندسي إلى أي زاوية تريدها. ما عليك سوى ضبط عملية التدوير على جيب الزاوية وجيب التمام للزاوية التي تريد التدوير إليها.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

نأمل أن تكون هذه المعلومات مفيدة. سنعرض لك مثالاً أبسط. الضبط.

ما هي الراديان؟

الراديان هي وحدة قياس تُستخدَم مع الدوائر والدوران والزوايا. تمامًا كما يمكننا قياس المسافة بالبوصة أو ياردة أو متر وما إلى ذلك، يمكننا قياس الزوايا بالدرجات أو الراديان.

من المرجّح أنّك على دراية بأنّ العمليات الحسابية باستخدام المقاييس المترية أسهل من العمليات الحسابية باستخدام المقاييس الإمبراطورية. للتحويل من البوصة إلى القدم، نقسم على 12. للتحويل من البوصة إلى ياردة، نقسم على 36. لا أعرف ما إذا كان بإمكانك إجراء عملية القسمة على 36 في ذهنك. باستخدام المقياس، يكون الأمر أسهل بكثير. للتحويل من ملليمترات إلى سنتيمترات، نقسم على 10. للتحويل من ملليمترات إلى متر، نقسم على 1000. أستطيع إجراء عملية القسمة على 1000 في ذهني.

تتشابه وحدات الراديان مع الدرجات. تجعل درجات الحرارة الحساب أكثر صعوبة. تسهّل الراديان العمليات الحسابية. هناك 360 درجة في الدائرة ولكن هناك راديان 2π فقط. وبالتالي، تكون الدورة الكاملة 2π راديان. نصف دورة تساوي π راديان. ربع دورة، أي 90 درجة، تساوي π/2 راديان. إذا أردت تدوير عنصر بزاوية 90 درجة، ما عليك سوى استخدام Math.PI * 0.5. إذا كنت تريد تدويره 45 درجة، استخدِم Math.PI * 0.25 وما إلى ذلك.

إنّ جميع العمليات الحسابية تقريبًا التي تتضمّن زوايا أو دوائر أو دورانًا تعمل ببساطة شديدة إذا بدأت التفكير بالراديان. لذا ننصحك بتجربة هذه الميزة. استخدِم وحدات الراديان، وليس الدرجات، باستثناء شاشات واجهة المستخدم.

مقياس WebGL ثنائي الأبعاد

ويمكنك توسيع نطاق استخدامها بسهولة مثل الترجمة.

نضرب الموضع في المقياس المطلوب. في ما يلي التغييرات التي أجريناها على العيّنة السابقة.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

ونضيف JavaScript المطلوب لضبط المقياس عند الرسم.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

يُرجى ملاحظة أنّ التكبير أو التصغير بقيمة سلبية يقلب الشكل الهندسي. نأمل أن تكون هذه الفصول الثلاثة الأخيرة مفيدة في فهم عمليات الترجمة والدوران والتكبير/التصغير. بعد ذلك، سنطّلع على سحر المصفوفات التي تجمع بين هذه العناصر الثلاثة في شكل أبسط بكثير وأكثر فائدة في أغلب الأحيان.

لماذا "F"؟

كانت المرة الأولى التي رأيت فيها شخصًا يستخدم الحرف "F" في نسيج. لا يهمّ الحرف "F" نفسه. من المهم أن تتمكّن من تحديد اتجاهه من أي اتجاه. على سبيل المثال، إذا استخدمنا قلبًا ♥ أو مثلثًا △، لن نتمكّن من معرفة ما إذا كان قد تم قلبه أفقيًا. سيكون استخدام دائرة ○ أسوأ. يمكن استخدام مستطيل ملون بألوان مختلفة في كل زاوية، ولكن عليك بعد ذلك تذكُّر الزاوية التي تشير إلى كل عنصر. يمكن التعرّف على اتجاه الحرف F على الفور.

يمكنك استخدام أي شكل يمكنك تحديد اتجاهه، وقد استخدمت حرف "F" منذ أن تم تعريفي على الفكرة.

مصفوفات ثنائية الأبعاد في WebGL

في الفصول الثلاثة الأخيرة، اطّلعنا على كيفية ترجمة الأشكال الهندسية وتدويرها وتغيير حجمها. يُعدّ كلّ من الترجمة والدوران والتكبير/التصغير نوعًا من "التحويل". كان كلّ من هذه التحولات يتطلّب إجراء تغييرات على برنامج تشويش الصورة، وكان كلّ من التحولات الثلاثة يعتمد على الترتيب.

على سبيل المثال، إليك مقياس 2، 1، ودرجة دوران 30%، وترجمة 100، 0.

في ما يلي ترجمة القيمة 100,0، ودرجة الدوران 30%، ودرجة التوسيع 2, 1

تختلف النتائج تمامًا. والأسوأ من ذلك، إذا احتجنا إلى المثال الثاني، علينا كتابة برنامج تشويش ألوان مختلف يطبّق الترجمة والدوران والتكبير/التصغير بالترتيب الجديد المطلوب. حسنًا، اكتشف بعض الأشخاص الأذكياء جدًا أنّه يمكنك إجراء كل الإجراءات نفسها باستخدام الرياضيات المصفوفية. بالنسبة إلى الصور ثنائية الأبعاد، نستخدم مصفوفة 3×3. المصفوفة 3×3 هي مثل شبكة تتضمّن 9 مربّعات.

1	2.0	3
4.0	5.0	6.0
7	من نظام التشغيل Android	9.0

لإجراء العمليات الحسابية، نضرب الموضع في أعمدة المصفوفة ونجمع النتائج. تحتوي مواضعنا على قيمتَين فقط، هما x وy، ولكن لإجراء هذا الحساب، نحتاج إلى 3 قيم، لذا سنستخدم القيمة 1 للقيمة الثالثة. في هذه الحالة، ستكون النتيجة على النحو التالي:

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

من المرجّح أنّك تنظر إلى ذلك وتسأل نفسك "ما الفائدة من ذلك؟". لنفترض أنّ لدينا ترجمة. سنُطلِق على المبلغ الذي نريد ترجمته tx وty. لننشئ مصفوفة مثل هذه

1	0.0	0.0
0.0	1	0.0
tx	ty	1

وننصحك بالاطّلاع على

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

إذا كنت تتذكر الجبر، يمكننا حذف أي مكان يُضرب فيه بصفر. لا يؤدي الضرب في 1 إلى أي نتيجة، لذا لنبسّط العملية لمعرفة ما يحدث.

newX = x + tx;
newY = y + ty;

ولا يهمّنا ذلك. يبدو أنّ هذا الرمز يشبه بشكل مفاجئ رمز الترجمة من مثال الترجمة. وبالمثل، لننفِّذ عملية الدوران. كما أوضحنا في مقالة التدوير، ما عليك سوى الحصول على جيب التمام وجيب الزاوية التي تريد تدويرها.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

وننشئ مصفوفة على النحو التالي:

c	-s	0.0
s	c	0.0
0.0	0.0	1

عند تطبيق المصفوفة، نحصل على ما يلي

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

بعد حجب كل عمليات الضرب بـ 0 و1، نحصل على

newX = x *  c + y * s;
newY = x * -s + y * c;

وهذا ما حدث بالضبط في عيّنة التناوب. وأخيرًا، التوسّع. سنُطلِق على عاملَي القياس اسمَي sx وsy ونُنشئ مصفوفة على النحو التالي

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1

عند تطبيق المصفوفة، نحصل على ما يلي

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

وهو أمر

newX = x * sx;
newY = y * sy;

وهي مطابقة لعينة التوسيع. الآن، أعلم أنّك لا تزال تفكر في الأمر. ماذا يعني ذلك؟ ما الفائدة من ذلك؟ يبدو أنّ هذا يتطلّب الكثير من العمل لإجراء الإجراء نفسه الذي كنا ننفّذه من قبل؟ هنا يأتي دور السحر. تبيّن لنا أنّه يمكننا ضرب المصفوفات معًا وتطبيق جميع عمليات التحويل دفعةً واحدة. لنفترض أنّ لدينا الدالة matrixMultiply التي تأخذ صفيفتَين وتضربهما وتُعرِض النتيجة. لتوضيح الأمور، لننشئ دوالّ لإنشاء مصفوفات للترجمة والدوران والتوسيع.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

لنغيّر الآن برنامج تشويش الصورة. كان مظهر مخطّط الألوان القديم على النحو التالي:

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

سيكون برنامج التظليل الجديد أكثر بساطة.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

في ما يلي كيفية استخدامنا لهذه البيانات:

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

قد تتساءل، ما الفائدة من ذلك؟ لا يبدو أنّ هذا يقدّم فائدة كبيرة . ولكن الآن، إذا أردنا تغيير الترتيب، لن نحتاج إلى كتابة برنامج تشويش جديد. يمكننا تغيير العملية الحسابية.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

إنّ إمكانية تطبيق مصفوفات مثل هذه مهمّة بشكل خاص للرسوم المتحركة التسلسلية، مثل الأذرع على الجسم أو الأقمار على كوكب حول الشمس أو الأغصان على الشجرة. للحصول على مثال بسيط على الصور المتحركة التسلسلية، لنرسم حرف "F" 5 مرات، ولكن لنبدأ في كل مرة بالمصفوفة من حرف "F" السابق.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

لإجراء ذلك، كان علينا تقديم الدالة makeIdentity التي تنشئ مصفوفة هوية. مصفوفة الهوية هي مصفوفة تمثّل بشكل فعّال 1.0 بحيث لا يحدث أي شيء في حال الضرب في الهوية. تمامًا مثل

X * 1 = X

كذلك

matrixX * identity = matrixX

في ما يلي الرمز البرمجي لإنشاء مصفوفة هوية.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

مثال آخر: في كل عيّنة حتى الآن، تدور الحرف "F" حول أعلى يمينها. ويعود السبب في ذلك إلى أنّ العمليات الحسابية التي نستخدمها تدور دائمًا حول نقطة الأصل، ويكون أعلى يمين "F" عند نقطة الأصل (0, 0). ولكن الآن، بما أنّه يمكننا إجراء عمليات حسابية للمصفوفات واختيار ترتيب تطبيق عمليات التحويل، يمكننا نقل نقطة الأصل قبل تطبيق بقية عمليات التحويل.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

باستخدام هذه الطريقة، يمكنك تدوير الصورة أو تغيير حجمها من أي نقطة. الآن، أنت تعرف كيف يتيح لك Photoshop أو Flash نقل نقطة الدوران. لنطّلِع على المزيد من التفاصيل. إذا رجعت إلى المقالة الأولى حول أساسيات WebGL، قد تتذكر أنّ لدينا رمزًا في برنامج التظليل للتحويل من البكسل إلى مساحة القصاصة التي تبدو على النحو التالي.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

إذا اطّلعت على كلّ خطوة من هذه الخطوات بدورها، ستلاحظ أنّ الخطوة الأولى، "التحويل من البكسل إلى 0.0 إلى 1.0"، هي في الواقع عملية توسيع. العملية الثانية هي أيضًا عملية تغيير حجم. العنصر التالي هو ترجمة، والعنصر الأخير يحوّل Y إلى -1. يمكننا فعل ذلك في المصفوفة التي نرسلها إلى برنامج التظليل. يمكننا إنشاء مصفوفتَي قياس، إحداهما لتوسيع النطاق بمقدار 1.0/درجة الدقة، والأخرى لتوسيع النطاق بمقدار 2.0، والثالثة للترجمة بمقدار -1.0، -1.0 والرابعة لتوسيع النطاق Y بمقدار -1، ثم ضربها معًا، ولكن بدلاً من ذلك، ولأنّ العمليات الحسابية بسيطة، سننشئ وظيفة تنشئ مصفوفة "إسقاط" لدرجة دقة معيّنة مباشرةً.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

يمكننا الآن تبسيط مخطّط الألوان أكثر. في ما يلي برنامج تشويش قمة جديد بالكامل.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

وفي JavaScript، علينا الضرب في مصفوفة الإسقاط.

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

وأزلنا أيضًا الرمز الذي يحدّد درجة الدقة. باستخدام هذه الخطوة الأخيرة، انتقلنا من مخطّط ألوان معقّد إلى مخطّط ألوان بسيط جدًا يتطلّب خطوة واحدة فقط، وذلك بفضل سحر الرياضيات المصفوفية.

نأمل أن تكون هذه المقالة قد ساعدت في توضيح الرياضيات المتعلقة بالمصفوفات. سأنتقل إلى القسم "الصور الثلاثية الأبعاد" بعد ذلك. في المصفوفات الثلاثية الأبعاد، تتبع الرياضيات المبادئ والاستخدامات نفسها. لقد بدأت باستخدام الصور ثنائية الأبعاد للحفاظ على بساطتها وسهولة فهمها.