Tłumaczenie 2D w WebGL
Zanim przejdziemy do 3D, jeszcze przez chwilę pozostańmy w 2D. Proszę o cierpliwość. Ten artykuł może się niektórym wydawać oczywisty, ale w kilku kolejnych artykułach przedstawię kilka przykładów.
Ten artykuł jest kontynuacją serii, która rozpoczęła się od artykułu Podstawy WebGL. Jeśli jeszcze tego nie zrobiłeś, przeczytaj przynajmniej pierwszy rozdział, a potem wracaj tutaj. Translation to skomplikowana nazwa matematyczna, która oznacza „przesunięcie” czegoś. Przenoszenie zdania z języka angielskiego na japoński też się nadaje, ale w tym przypadku mówimy o przenoszeniu geometrii. Za pomocą przykładowego kodu z pierwszego wpisu można łatwo przesunąć prostokąt, zmieniając wartości przekazane do setRectangle. Oto przykład na podstawie poprzedniego przykładu.
// First lets make some variables
// to hold the translation of the rectangle
var translation = [0, 0];
// then let's make a function to
// re-draw everything. We can call this
// function after we update the translation.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Setup a rectangle
setRectangle(gl, translation[0], translation[1], width, height);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 6);
}
Idzie Ci dobrze. Teraz wyobraź sobie, że chcemy zrobić to samo z bardziej skomplikowanym kształtem. Załóżmy, że chcemy narysować literę „F” składającą się z 6 trójkątów, takich jak ten.
Oto obecny kod, w którym musimy zmienić setRectangle na coś takiego.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
var width = 100;
var height = 150;
var thickness = 30;
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
x, y,
x + thickness, y,
x, y + height,
x, y + height,
x + thickness, y,
x + thickness, y + height,
// top rung
x + thickness, y,
x + width, y,
x + thickness, y + thickness,
x + thickness, y + thickness,
x + width, y,
x + width, y + thickness,
// middle rung
x + thickness, y + thickness * 2,
x + width * 2 / 3, y + thickness * 2,
x + thickness, y + thickness * 3,
x + thickness, y + thickness * 3,
x + width * 2 / 3, y + thickness * 2,
x + width * 2 / 3, y + thickness * 3]),
gl.STATIC_DRAW);
}
Mam nadzieję, że widzisz, że nie da się tego dobrze skalować. Jeśli chcemy narysować bardzo złożoną geometrię z setkami lub tysiącami linii, musimy napisać dość skomplikowany kod. Co więcej, za każdym razem, gdy rysujemy, JavaScript musi aktualizować wszystkie punkty. Jest prostszy sposób. Wystarczy przesłać geometrię i przeprowadzić tłumaczenie w shaderze. Oto nowy shader
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
void main() {
// Add in the translation.
vec2 position = a_position + u_translation;
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
...
i nieco zmienimy w kodzie. Po pierwsze, geometrię trzeba ustawić tylko raz.
// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
gl.bufferData(
gl.ARRAY_BUFFER,
new Float32Array([
// left column
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
// top rung
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
// middle rung
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90]),
gl.STATIC_DRAW);
}
Następnie przed narysowaniem żądanego tłumaczenia musimy zaktualizować u_translation.
...
var translationLocation = gl.getUniformLocation(
program, "u_translation");
...
// Set Geometry.
setGeometry(gl);
..
// Draw scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Funkcja notice setGeometry jest wywoływana tylko raz. Nie znajduje się już w drawScene.
Teraz, gdy rysujemy, WebGL robi praktycznie wszystko. Wszystko, co robimy, to ustawiamy tłumaczenie i prosimy o narysowanie. Nawet jeśli geometria miałaby dziesiątki tysięcy punktów, kod główny pozostawałby taki sam.
Obrót 2D w WebGL
Od razu przyznam, że nie mam pojęcia, czy to, co chcę wyjaśnić, ma sens, ale spróbuję.
Najpierw chcę Ci przedstawić tzw. „okrąg jednostkowy”. Jeśli pamiętasz matematykę z podstawówki (nie zasypiaj!), wiesz, że okrąg ma promień. Promień koła to odległość od środka koła do jego krawędzi. Okrąg jednostkowy to okrąg o promieniu równym 1,0.
Jeśli pamiętasz podstawy matematyki z 3 klasy, wiesz, że mnożenie przez 1 nie zmienia wartości. W związku z tym 123 × 1 = 123. To dość proste, prawda? Okrąg jednostkowy, czyli okrąg o promieniu 1,0, jest też formą 1. Jest to liczba 1, która się obraca. Możesz pomnożyć coś przez ten okrąg jednostkowy. W pewnym sensie jest to jak mnożenie przez 1, ale z tym, że działa magia i wszystko się obraca. Weźmiemy wartości X i Y z dowolnego punktu na kole jednostkowym i pomnożymy naszą geometrię przez nie z poprzedniego przykładu. Oto zmiany w naszym shaderze.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
void main() {
// Rotate the position
vec2 rotatedPosition = vec2(
a_position.x * u_rotation.y + a_position.y * u_rotation.x,
a_position.y * u_rotation.y - a_position.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
Zaktualizowaliśmy kod JavaScript, aby można było przekazać te 2 wartości.
...
var rotationLocation = gl.getUniformLocation(program, "u_rotation");
...
var rotation = [0, 1];
..
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Dlaczego to działa? Spójrz na obliczenia.
rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;
Załóżmy, że masz prostokąt i chcesz go obrócić. Zanim zaczniesz obracać, prawy górny róg ma wartość 3,0, 9,0. Wybierzmy punkt na kole jednostkowym, który znajduje się 30° w kierunku ruchu wskazówek zegara od godziny 12.
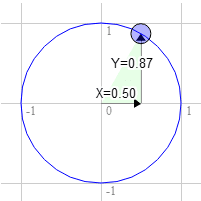
Pozycja na kole to 0,50 i 0,87
3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3
To jest dokładnie to, czego potrzebujemy
To samo w przypadku 60 stopni w prawo
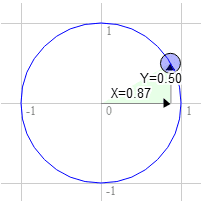
Pozycja na kole to 0,87 i 0,50
3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9
Gdy obracasz ten punkt zgodnie z kierunkiem ruchu wskazówek zegara, wartość X rośnie, a wartość Y maleje. Jeśli spróbujemy przesunąć wskaźnik poza 90°, X zacznie się zmniejszać, a Y – zwiększać. Ten wzór zapewnia nam rotację. Punkty na okręgu jednostkowym mają inną nazwę. Nazywa się je sinusem i cosinusem. W przypadku dowolnego kąta możemy w ten sposób sprawdzić sinus i cosinus.
function printSineAndCosineForAnAngle(angleInDegrees) {
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);
console.log("s = " + s + " c = " + c);
}
Jeśli skopiujesz kod i wkleisz go w konsoli JavaScriptu, a potem wpiszesz printSineAndCosignForAngle(30), zobaczysz, że wypisuje się s = 0.49 c= 0.87 (uwaga: zaokrągliłem liczby).
Po połączeniu wszystkich tych elementów możesz obracać geometrię pod dowolnym kątem. Wystarczy, że ustawisz obrót na sinus i cosinus kąta, pod którym chcesz go wykonać.
...
var angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.sin(angleInRadians);
rotation[1] = Math.cos(angleInRadians);
Mam nadzieję, że to wyjaśnia sprawę. A teraz prostsza wersja. Skalowanie:
Czym są radiany?
Radiansy to jednostka miary używana w przypadku kół, obrotów i kątów. Podobnie jak możemy mierzyć odległość w calach, jardach, metrach itp., możemy mierzyć kąty w stopniach lub radianach.
Prawdopodobnie wiesz, że obliczenia z użyciem miar metrycznych są łatwiejsze niż z użyciem miar imperialnych. Aby przeliczyć cale na stopy, dzielimy przez 12. Aby przeliczyć cale na jardy, dzielimy przez 36. Nie wiem, jak Ty, ale ja nie potrafię dzielić przez 36 w głowie. W przypadku danych liczbowych jest to znacznie łatwiejsze. Aby przejść z milimetrów na centymetry, dzielimy przez 10. Aby przeliczyć milimetry na metry, dzielimy przez 1000. Mogę podzielić 1000 w głowie.
Radiany i stopnie są podobne. Stopnie utrudniają obliczenia. Radiansy ułatwiają obliczenia. Krąg ma 360°, ale tylko 2π rad. Pełny obrót to 2π rad. Półobrot to π rad. 1/4 obrócenia, czyli 90 stopni to π/2 radianów. Jeśli więc chcesz obrócić coś o 90 stopni, użyj Math.PI * 0.5. Jeśli chcesz obrócić obraz o 45°, użyj Math.PI * 0.25 itp.
Prawie wszystkie obliczenia dotyczące kątów, okręgów lub obrotu są bardzo proste, jeśli zaczniesz myśleć w radianach. Wypróbuj. Używaj radianów, a nie stopni, z wyjątkiem wyświetlania w interfejsie.
Skala 2D WebGL
Skalowanie jest tak samo proste jak tłumaczenie.
Pozycję mnożymy przez wybraną skalę. Oto zmiany w poprzednim pliku.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y +
scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y -
scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
i dodajemy kod JavaScript potrzebny do ustawienia skali podczas rysowania.
...
var scaleLocation = gl.getUniformLocation(program, "u_scale");
...
var scale = [1, 1];
...
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Set the translation.
gl.uniform2fv(translationLocation, translation);
// Set the rotation.
gl.uniform2fv(rotationLocation, rotation);
// Set the scale.
gl.uniform2fv(scaleLocation, scale);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Warto zauważyć, że skalowanie o wartość ujemną odwraca geometrię. Mam nadzieję, że te 3 ostatnie rozdziały pomogły Ci zrozumieć przekształcenia liniowe, rotacje i skale. Następnie omówimy magię, jaką są macierze, które łączą wszystkie 3 te elementy w znacznie prostszą i często przydatną formę.
Dlaczego „F”?
Po raz pierwszy zobaczyłem, jak ktoś używa „F” w teksturze. Samo „F” nie ma znaczenia. Ważne jest to, że możesz określić jego orientację z dowolnego kierunku. Jeśli użylibyśmy na przykład serca ♥ lub trójkąta △, nie moglibyśmy stwierdzić, czy zostały odwrócone poziomo. Okrąg ○ byłby jeszcze gorszy. Kolorowy prostokąt z różnymi kolorami na każdym rogu też byłby dobry, ale trzeba by pamiętać, który róg jest który. Litera F jest od razu rozpoznawalna.
Każdy kształt, który ma określoną orientację, będzie odpowiedni. Odkąd po raz pierwszy usłyszałem o tej idei, używam litery „F”.
Macierze 2D WebGL
W 3 ostatnich rozdziałach omawialiśmy przesuwanie, obracanie i skalowanie geometrii. Przesunięcie, obrót i skala są uważane za rodzaj „przekształcenia”. Każda z tych przekształceń wymagała wprowadzenia zmian w shaderze, a każda z 3 przekształceń była zależna od kolejności.
Na przykład: powiększenie 2, 1, obrót o 30% i przesunięcie o 100, 0.
A tutaj przesunięcie 100,0, obrót 30% i skala 2, 1
Wyniki są zupełnie inne. Co gorsza, gdybyśmy potrzebowali drugiego przykładu, musielibyśmy napisać inny shader, który zastosowałby przesunięcie, obrót i powiększenie w nowym żądanym porządku. Niektórzy ludzie, którzy są znacznie mądrzejsi ode mnie, odkryli, że można robić to samo za pomocą obliczeń macierzowych. W przypadku obrazu 2D używamy macierzy 3 x 3. Macierz 3 x 3 to siatka z 9 polem.
| 1,0 | 2,0 | 3,0 |
| 4.0 | 5,0 | 6,0 |
| 7.0 | z Androidem 8.0 | 9.0 |
Aby to zrobić, mnożymy pozycję po kolumnach macierzy i sumujemy wyniki. Nasze pozycje mają tylko 2 wartości: x i y, ale do wykonania tych obliczeń potrzebujemy 3 wartości, więc jako trzeciej użyjemy 1. W tym przypadku nasz wynik będzie wynosił
newX = x * 1.0 + y * 4.0 + 1 * 7.0
newY = x * 2.0 + y * 5.0 + 1 * 8.0
extra = x * 3.0 + y * 6.0 + 1 * 9.0
Prawdopodobnie zastanawiasz się, o co w ogóle chodzi. Załóżmy, że mamy tłumaczenie. Nazwa kwoty, którą chcemy przetłumaczyć, to tx i ty. Utwórz taką macierz
| 1,0 | 0,0 | 0,0 |
| 0,0 | 1,0 | 0,0 |
| tx | ty | 1,0 |
A teraz zobacz
newX = x * 1.0 + y * 0.0 + 1 * tx
newY = x * 0.0 + y * 1.0 + 1 * ty
extra = x * 0.0 + y * 0.0 + 1 * 1
Jeśli pamiętasz algebrę, możesz usunąć dowolne miejsce, które mnoży się przez zero. Pomnożenie przez 1 nie powoduje żadnych zmian, więc uprośćmy obliczenia, aby zobaczyć, co się dzieje
newX = x + tx;
newY = y + ty;
A dodatkowe nie są nam tak naprawdę potrzebne. Wygląda to zaskakująco podobnie do kodu tłumaczenia z naszego przykładu. Zróbmy to samo z rotacją. Jak wspomnieliśmy w poście na temat rotacji, potrzebujemy tylko sinusa i cosinusa kąta, pod jakim chcemy obrócić obiekt.
s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);
Tworzymy macierz w takiej postaci:
| C | -s | 0,0 |
| s | C | 0,0 |
| 0,0 | 0,0 | 1,0 |
Po zastosowaniu macierzy otrzymujemy
newX = x * c + y * s + 1 * 0
newY = x * -s + y * c + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
Po zastąpieniu wszystkich mnożeń przez 0 i 1 otrzymujemy
newX = x * c + y * s;
newY = x * -s + y * c;
Właśnie to mieliśmy w próbce rotacji. I na koniec skala. Nasze 2 współczynniki skali będą nazywać sx i sy. Tworzymy taką oto tablicę.
| sx | 0,0 | 0,0 |
| 0,0 | sy | 0,0 |
| 0,0 | 0,0 | 1,0 |
Po zastosowaniu macierzy otrzymujemy
newX = x * sx + y * 0 + 1 * 0
newY = x * 0 + y * sy + 1 * 0
extra = x * 0.0 + y * 0.0 + 1 * 1
co jest naprawdę
newX = x * sx;
newY = y * sy;
Jest to to samo co w przypadku przykładu skalowania.
Pewnie nadal się zastanawiasz. Co z tego? O co chodzi? To wydaje się dużo pracy, żeby robić to samo, co robiliśmy do tej pory.
Tutaj zaczyna się magia. Okazuje się, że możemy pomnożyć macierze i zastosować wszystkie przekształcenia jednocześnie. Załóżmy, że mamy funkcję matrixMultiply, która przyjmuje 2 macierze, mnoży je i zwraca wynik.
Aby to wyjaśnić, utwórzmy funkcje do tworzenia macierzy przekształceń przesunięcia, obrotu i skalowania.
function makeTranslation(tx, ty) {
return [
1, 0, 0,
0, 1, 0,
tx, ty, 1
];
}
function makeRotation(angleInRadians) {
var c = Math.cos(angleInRadians);
var s = Math.sin(angleInRadians);
return [
c,-s, 0,
s, c, 0,
0, 0, 1
];
}
function makeScale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
];
}
Zmieńmy teraz shader. Stary shader wyglądał tak
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;
void main() {
// Scale the positon
vec2 scaledPosition = a_position * u_scale;
// Rotate the position
vec2 rotatedPosition = vec2(
scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);
// Add in the translation.
vec2 position = rotatedPosition + u_translation;
...
Nasz nowy shader będzie znacznie prostszy.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
vec2 position = (u_matrix * vec3(a_position, 1)).xy;
...
Oto jak to robimy
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix =
makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the rectangle.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
Możesz jednak zapytać, co z tego wynika. To nie jest duża korzyść . Teraz, jeśli chcemy zmienić kolejność, nie musimy pisać nowego shadera. Możemy zmienić tylko sposób obliczania.
...
// Multiply the matrices.
var matrix = matrixMultiply(translationMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, scaleMatrix);
...
Możliwość stosowania takich macierzy jest szczególnie ważna w przypadku animacji hierarchicznej, np. ramion na ciele, księżyców na orbicie wokół słońca czy gałęzi na drzewie. W prostym przykładzie animacji hierarchicznej narysujemy 5 razy literę „F”, ale za każdym razem zaczniemy od macierzy z poprzedniej litery „F”.
// Draw the scene.
function drawScene() {
// Clear the canvas.
gl.clear(gl.COLOR_BUFFER_BIT);
// Compute the matrices
var translationMatrix = makeTranslation(translation[0], translation[1]);
var rotationMatrix = makeRotation(angleInRadians);
var scaleMatrix = makeScale(scale[0], scale[1]);
// Starting Matrix.
var matrix = makeIdentity();
for (var i = 0; i < 5; ++i) {
// Multiply the matrices.
matrix = matrixMultiply(matrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
// Set the matrix.
gl.uniformMatrix3fv(matrixLocation, false, matrix);
// Draw the geometry.
gl.drawArrays(gl.TRIANGLES, 0, 18);
}
}
W tym celu wprowadziliśmy funkcję makeIdentity, która tworzy macierz tożsamości. Macierz jednostkowa to macierz, która w efekcie reprezentuje wartość 1,0, więc jeśli pomnożysz ją przez macierz jednostkową, nic się nie stanie.
X * 1 = X
tak samo
matrixX * identity = matrixX
Oto kod służący do tworzenia macierzy tożsamości.
function makeIdentity() {
return [
1, 0, 0,
0, 1, 0,
0, 0, 1
];
}
Jeszcze jeden przykład. We wszystkich dotychczasowych próbkach litera „F” obraca się wokół lewego górnego rogu. Dzieje się tak, ponieważ używamy obliczeń, które zawsze obracają wokół punktu wyjścia, a lewy górny róg obiektu „F” znajduje się w punkcie wyjścia (0, 0). Teraz, ponieważ możemy wykonywać obliczenia macierzy i wybierać kolejność, w jakiej mają być stosowane przekształcenia, możemy przesunąć punkt wyjścia przed zastosowaniem pozostałych przekształceń.
// make a matrix that will move the origin of the 'F' to
// its center.
var moveOriginMatrix = makeTranslation(-50, -75);
...
// Multiply the matrices.
var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
matrix = matrixMultiply(matrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
Dzięki tej metodzie możesz obracać lub skalować obiekt z dowolnego miejsca. Wiesz już, jak w Photoshopie lub Flashu można przesuwać punkt obrotu. Zróbmy coś jeszcze bardziej szalonego. Jeśli wrócisz do pierwszego artykułu o podstawach WebGL, możesz pamiętać, że w shaderze mamy kod do konwersji z pikseli na przestrzeń ścinki, który wygląda tak:
...
// convert the rectangle from pixels to 0.0 to 1.0
vec2 zeroToOne = position / u_resolution;
// convert from 0->1 to 0->2
vec2 zeroToTwo = zeroToOne * 2.0;
// convert from 0->2 to -1->+1 (clipspace)
vec2 clipSpace = zeroToTwo - 1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
Jeśli przyjrzysz się po kolei poszczególnym krokom, zauważysz, że pierwszy z nich, czyli „konwersja z pikseli na 0,0–1,0”, jest operacją skalowania. Druga to również operacja skali. Kolejny to przesunięcie, a ostatni przeskalowanie Y o -1. Możemy to zrobić w ramach macierzy przekazywanej do shadera. Możemy utworzyć 2 macierze skalowania: jedną do skalowania o 1,0/rozdzielczość, drugą do skalowania o 2,0, trzecią do przesunięcia o -1,0,-1.0 i czwartą do skalowania Y o -1, a następnie pomnożyć je wszystkie razem. Ponieważ jednak obliczenia są proste, zamiast tego utworzymy funkcję, która bezpośrednio tworzy „rzutowanie” macierzy dla danej rozdzielczości.
function make2DProjection(width, height) {
// Note: This matrix flips the Y axis so that 0 is at the top.
return [
2 / width, 0, 0,
0, -2 / height, 0,
-1, 1, 1
];
}
Teraz możemy jeszcze bardziej uprościć shader. Oto cały nowy shader wierzchołkowy.
<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;
uniform mat3 u_matrix;
void main() {
// Multiply the position by the matrix.
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>
W JavaScript musimy pomnożyć przez macierz projekcji
// Draw the scene.
function drawScene() {
...
// Compute the matrices
var projectionMatrix =
make2DProjection(canvas.width, canvas.height);
...
// Multiply the matrices.
var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
matrix = matrixMultiply(matrix, translationMatrix);
matrix = matrixMultiply(matrix, projectionMatrix);
...
}
Usunęliśmy też kod, który ustawiał rozdzielczość. Dzięki temu ostatniemu krokowi udało nam się przejść od dość skomplikowanego shadera z 6–7 krokami do bardzo prostego shadera z jedynym krokiem. Wszystko dzięki magii obliczeń macierzy.
Mam nadzieję, że ten artykuł pomógł Ci zrozumieć matematykę macierzy. Teraz przejdę do 3D. W przypadku macierzy 3D matematyka działa według tych samych zasad i w taki sam sposób. Zacząłem od 2D, aby ułatwić zrozumienie.