WebGL تبدیل می شود

Gregg Tavares

ترجمه دو بعدی WebGL

قبل از اینکه به سمت سه بعدی برویم، اجازه دهید برای مدتی بیشتر به دو بعدی بپردازیم. تحمل کن لطفا این مقاله ممکن است برای برخی بسیار بدیهی به نظر برسد، اما من در چند مقاله به یک نقطه می پردازم.

این مقاله ادامه مجموعه‌ای است که با WebGL Fundamentals شروع می‌شود. اگر آن را نخوانده اید، پیشنهاد می کنم حداقل فصل اول را بخوانید و سپس به اینجا بازگردید. ترجمه یک نام ریاضی فانتزی است که اساساً به معنای "حرکت دادن" چیزی است. من فکر می کنم جابجایی یک جمله از انگلیسی به ژاپنی نیز مناسب است، اما در این مورد ما در مورد هندسه متحرک صحبت می کنیم. با استفاده از کد نمونه ای که در پست اول به پایان رسید، می توانید به راحتی مستطیل ما را فقط با تغییر مقادیر ارسال شده به setRectangle ترجمه کنید درست است؟ در اینجا یک نمونه بر اساس نمونه قبلی ما آمده است.

  // First lets make some variables 
  // to hold the translation of the rectangle
  var translation = [0, 0];
  // then let's make a function to
  // re-draw everything. We can call this
  // function after we update the translation.
  // Draw the scene.
  function drawScene() {
     // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);
    // Setup a rectangle
    setRectangle(gl, translation[0], translation[1], width, height);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }

تا اینجای کار خیلی خوبه. اما حالا تصور کنید می‌خواهیم همین کار را با شکل پیچیده‌تری انجام دهیم. فرض کنید می‌خواستیم یک «F» بکشیم که از 6 مثلث تشکیل شده است.

خوب، در زیر کدهای فعلی وجود دارد که ما باید setRectangle را به چیزی شبیه به این تغییر دهیم.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl, x, y) {
  var width = 100;
  var height = 150;
  var thickness = 30;
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          x, y,
          x + thickness, y,
          x, y + height,
          x, y + height,
          x + thickness, y,
          x + thickness, y + height,

          // top rung
          x + thickness, y,
          x + width, y,
          x + thickness, y + thickness,
          x + thickness, y + thickness,
          x + width, y,
          x + width, y + thickness,

          // middle rung
          x + thickness, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 2,
          x + thickness, y + thickness * 3,
          x + thickness, y + thickness * 3,
          x + width * 2 / 3, y + thickness * 2,
          x + width * 2 / 3, y + thickness * 3]),
      gl.STATIC_DRAW);
}

امیدواریم ببینید که مقیاس خوبی نخواهد داشت. اگر بخواهیم هندسه بسیار پیچیده ای را با صدها یا هزاران خط رسم کنیم، باید کد بسیار پیچیده ای بنویسیم. علاوه بر این، هر بار که جاوا اسکریپت را ترسیم می کنیم باید تمام نقاط را به روز کند. راه ساده تری هم هست فقط هندسه را آپلود کنید و ترجمه را در سایه زن انجام دهید. در اینجا سایه زن جدید است

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;

void main() {
   // Add in the translation.
   vec2 position = a_position + u_translation;

   // convert the rectangle from pixels to 0.0 to 1.0
   vec2 zeroToOne = position / u_resolution;
   ...

و ما کد را کمی بازسازی می کنیم. برای یکی ما فقط باید یک بار هندسه را تنظیم کنیم.

// Fill the buffer with the values that define a letter 'F'.
function setGeometry(gl) {
  gl.bufferData(
      gl.ARRAY_BUFFER,
      new Float32Array([
          // left column
          0, 0,
          30, 0,
          0, 150,
          0, 150,
          30, 0,
          30, 150,

          // top rung
          30, 0,
          100, 0,
          30, 30,
          30, 30,
          100, 0,
          100, 30,

          // middle rung
          30, 60,
          67, 60,
          30, 90,
          30, 90,
          67, 60,
          67, 90]),
      gl.STATIC_DRAW);
}

سپس ما فقط باید u_translation قبل از ترسیم با ترجمه مورد نظر خود به روز کنیم.

  ...
  var translationLocation = gl.getUniformLocation(
             program, "u_translation");
  ...
  // Set Geometry.
  setGeometry(gl);
  ..
  // Draw scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

توجه کنید setGeometry فقط یک بار فراخوانی می شود. دیگر داخل drawScene نیست.

اکنون وقتی WebGL را ترسیم می کنیم عملاً همه چیز را انجام می دهد. تمام کاری که ما انجام می دهیم این است که یک ترجمه تنظیم می کنیم و از آن می خواهیم نقاشی کند. حتی اگر هندسه ما ده ها هزار نقطه داشته باشد، کد اصلی ثابت می ماند.

چرخش دو بعدی WebGL

می‌خواهم اعتراف کنم که نمی‌دانم چگونه این را توضیح می‌دهم یا نه، اما چه چیزی را می‌توان امتحان کرد.

ابتدا می‌خواهم شما را با چیزی که «دایره واحد» نامیده می‌شود آشنا کنم. اگر ریاضی دبیرستان خود را به خاطر دارید (به من نخوابید!) یک دایره شعاع دارد. شعاع دایره فاصله مرکز دایره تا لبه است. دایره واحد دایره ای با شعاع 1.0 است.

اگر از ریاضی پایه سوم ابتدایی یادتان باشد اگر چیزی را در 1 ضرب کنید ثابت می ماند. بنابراین 123 * 1 = 123. خیلی اساسی درست است؟ خوب، یک دایره واحد، یک دایره با شعاع 1.0 نیز به شکل 1 است. این یک 1 چرخشی است. بنابراین شما می توانید چیزی را در این دایره واحد ضرب کنید و به نوعی شبیه ضرب در 1 است به جز اینکه جادو اتفاق می افتد و چیزهایی اتفاق می افتد. چرخاندن ما آن مقدار X و Y را از هر نقطه از دایره واحد می گیریم و هندسه خود را در آنها از نمونه قبلی خود ضرب می کنیم. در اینجا به‌روزرسانی‌های شیدر ما آمده است.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;

void main() {
  // Rotate the position
  vec2 rotatedPosition = vec2(
     a_position.x * u_rotation.y + a_position.y * u_rotation.x,
     a_position.y * u_rotation.y - a_position.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

و ما جاوا اسکریپت را به روز می کنیم تا بتوانیم آن 2 مقدار را به آن منتقل کنیم.

  ...
  var rotationLocation = gl.getUniformLocation(program, "u_rotation");
  ...
  var rotation = [0, 1];
  ..
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

چرا کار می کند؟ خوب، به ریاضی نگاه کنید.

rotatedX = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
rotatedY = a_position.y * u_rotation.y - a_position.x * u_rotation.x;

بیایید بمانیم شما یک مستطیل دارید و می خواهید آن را بچرخانید. قبل از شروع چرخاندن آن، گوشه سمت راست بالای 3.0، 9.0 است. بیایید از ساعت 12 نقطه ای از دایره واحد را 30 درجه در جهت عقربه های ساعت انتخاب کنیم.

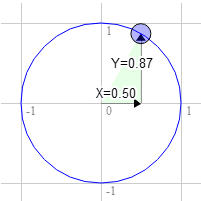
موقعیت روی دایره در آنجا 0.50 و 0.87 است

3.0 * 0.87 + 9.0 * 0.50 = 7.1
9.0 * 0.87 - 3.0 * 0.50 = 6.3

دقیقاً همان جایی است که ما به آن نیاز داریم

همینطور برای 60 درجه در جهت عقربه های ساعت

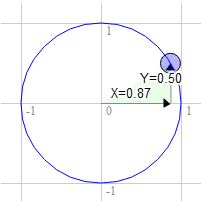
موقعیت روی دایره در آنجا 0.87 و 0.50 است

3.0 * 0.50 + 9.0 * 0.87 = 9.3
9.0 * 0.50 - 3.0 * 0.87 = 1.9

می بینید که وقتی آن نقطه را در جهت عقربه های ساعت به سمت راست می چرخانیم، مقدار X بزرگتر و Y کوچکتر می شود. اگر از 90 درجه گذشته بود X دوباره کوچکتر می شد و Y شروع به بزرگتر شدن می کرد. آن الگو به ما چرخش می دهد. نام دیگری برای نقاط روی دایره واحد وجود دارد. به آنها سینوس و کسینوس می گویند. بنابراین برای هر زاویه ای می توانیم سینوس و کسینوس را به این صورت جستجو کنیم.

function printSineAndCosineForAnAngle(angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180;
  var s = Math.sin(angleInRadians);
  var c = Math.cos(angleInRadians);
  console.log("s = " + s + " c = " + c);
}

اگر کد را در کنسول جاوا اسکریپت خود کپی و جایگذاری کنید و printSineAndCosignForAngle(30) تایپ کنید، می بینید که s = 0.49 c= 0.87 چاپ می شود (توجه: من اعداد را گرد کردم.) اگر همه آن ها را کنار هم قرار دهید، می توانید هندسه خود را به هر کدام بچرخانید. زاویه مورد نظر شما فقط چرخش را روی سینوس و کسینوس زاویه ای که می خواهید به آن بچرخانید تنظیم کنید.

  ...
  var angleInRadians = angleInDegrees * Math.PI / 180;
  rotation[0] = Math.sin(angleInRadians);
  rotation[1] = Math.cos(angleInRadians);

امیدوارم تا حدودی منطقی بوده باشد. بعدی ساده تر. مقیاس.

رادیان چیست؟

رادیان ها واحد اندازه گیری هستند که با دایره، چرخش و زاویه استفاده می شود. همانطور که می توانیم فاصله را بر حسب اینچ، یارد، متر و غیره اندازه گیری کنیم، می توانیم زاویه ها را بر حسب درجه یا رادیان اندازه گیری کنیم.

احتمالاً می‌دانید که ریاضی با اندازه‌گیری‌های متریک آسان‌تر از ریاضی با اندازه‌گیری‌های امپریالیستی است. برای رفتن از اینچ به پا، تقسیم بر 12 می کنیم. برای رفتن از اینچ به یارد، تقسیم بر 36 می کنیم. من در مورد شما نمی دانم اما من نمی توانم در ذهنم بر 36 تقسیم کنم. با متریک بسیار ساده تر است. برای رفتن از میلی متر به سانتی متر بر 10 تقسیم می کنیم. از میلی متر به متر بر 1000 تقسیم می کنیم.

رادیان ها و درجه ها مشابه هستند. مدرک ریاضی را سخت می کند. رادیان ها ریاضی را آسان می کنند. در یک دایره 360 درجه وجود دارد اما فقط 2π رادیان وجود دارد. بنابراین یک چرخش کامل 2π رادیان است. نیم چرخش π رادیان است. یک دور 1/4، یعنی 90 درجه، π/2 رادیان است. بنابراین اگر می خواهید چیزی را 90 درجه بچرخانید فقط از Math.PI * 0.5 استفاده کنید. اگر می خواهید آن را 45 درجه بچرخانید از Math.PI * 0.25 و غیره استفاده کنید.

تقریباً تمام ریاضیات مربوط به زوایا، دایره‌ها یا چرخش بسیار ساده عمل می‌کنند، اگر شروع کنید به رادیان فکر کنید. پس امتحانش کن از رادیان استفاده کنید، نه درجه به جز در نمایشگرهای UI.

مقیاس دو بعدی WebGL

مقیاس بندی به همان راحتی ترجمه است.

موقعیت را در مقیاس مورد نظر خود ضرب می کنیم. در اینجا تغییرات نسبت به نمونه قبلی ما آمده است.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y +
        scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y -
        scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;

و جاوا اسکریپت مورد نیاز برای تنظیم مقیاس هنگام ترسیم را اضافه می کنیم.

  ...
  var scaleLocation = gl.getUniformLocation(program, "u_scale");
  ...
  var scale = [1, 1];
  ...
  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Set the translation.
    gl.uniform2fv(translationLocation, translation);

    // Set the rotation.
    gl.uniform2fv(rotationLocation, rotation);

    // Set the scale.
    gl.uniform2fv(scaleLocation, scale);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

نکته ای که باید به آن توجه کرد این است که مقیاس بندی با مقدار منفی هندسه ما را تغییر می دهد. امیدوارم این 3 فصل آخر برای درک ترجمه، چرخش و مقیاس مفید بوده باشد. در ادامه به ماتریس‌هایی می‌پردازیم که هر 3 مورد را به شکلی بسیار ساده‌تر و اغلب مفیدتر ترکیب می‌کنند.

چرا "F"؟

اولین باری که دیدم کسی از "F" استفاده می کند روی یک بافت بود. F به خودی خود مهم نیست. آنچه مهم است این است که شما می توانید جهت آن را از هر جهتی تشخیص دهید. اگر از قلب ♥ یا مثلث △ استفاده می‌کردیم، نمی‌توانستیم تشخیص دهیم که به صورت افقی برگردانده شده است یا خیر. یک دایره ○ حتی بدتر خواهد بود. مسلماً یک مستطیل رنگی با رنگ های مختلف در هر گوشه کار می کند، اما پس از آن باید به یاد داشته باشید که کدام گوشه کدام گوشه است. جهت یک F فوراً قابل تشخیص است.

هر شکلی که بتوانید جهت آن را بگویید کار می کند، من از زمانی که برای اولین بار با این ایده آشنا شدم از "F" استفاده کردم.

ماتریس های دو بعدی WebGL

در 3 فصل آخر به چگونگی ترجمه هندسه، چرخش هندسه و هندسه مقیاس پرداختیم. ترجمه، چرخش و مقیاس هر کدام نوعی «تبدیل» در نظر گرفته می‌شوند. هر یک از این تبدیل ها نیاز به تغییراتی در سایه زن داشت و هر یک از 3 تبدیل به ترتیب وابسته بودند.

به عنوان مثال در اینجا یک مقیاس 2، 1، چرخش 30٪ و ترجمه 100، 0 است.

و در اینجا ترجمه 100،0، چرخش 30٪ و مقیاس 2، 1 است.

نتایج کاملا متفاوت است. حتی بدتر از آن، اگر به مثال دوم نیاز داشتیم، باید یک سایه زن متفاوت بنویسیم که ترجمه، چرخش و مقیاس را به ترتیب دلخواه جدید ما اعمال کند. خب، برخی از افراد بسیار باهوش‌تر از من، متوجه شدند که شما می‌توانید همه کارهای مشابه را با ریاضیات ماتریسی انجام دهید. برای 2d ما از یک ماتریس 3x3 استفاده می کنیم. یک ماتریس 3x3 مانند شبکه ای با 9 جعبه است.

1.0	2.0	3.0
4.0	5.0	6.0
7.0	8.0	9.0

برای انجام محاسبات، موقعیت را در ستون های ماتریس ضرب می کنیم و نتایج را جمع می کنیم. موقعیت های ما فقط 2 مقدار دارند، x و y، اما برای انجام این ریاضی به 3 مقدار نیاز داریم، بنابراین از 1 برای مقدار سوم استفاده می کنیم. در این صورت نتیجه ما خواهد بود

newX = x * 1.0 + y * 4.0 + 1 * 7.0

newY = x * 2.0 + y * 5.0 + 1 * 8.0

extra = x * 3.0 + y * 6.0 + 1 * 9.0

شما احتمالاً به آن نگاه می کنید و فکر می کنید "نکته چیست". خب، فرض کنیم ترجمه داریم. مقداری را که می‌خواهیم ترجمه کنیم tx و ty صدا می‌زنیم. بیایید یک ماتریس مانند این بسازیم

1.0	0.0	0.0
0.0	1.0	0.0
tx	ty	1.0

و حالا آن را بررسی کنید

newX = x * 1.0 + y * 0.0 + 1 * tx

newY = x * 0.0 + y * 1.0 + 1 * ty

extra = x * 0.0 + y * 0.0 + 1 * 1

اگر جبر خود را به خاطر دارید، می توانیم هر مکانی را که در صفر ضرب می شود حذف کنیم. ضرب در 1 به طور مؤثر هیچ کاری نمی کند، بنابراین بیایید ساده کنیم تا ببینیم چه اتفاقی می افتد

newX = x + tx;
newY = y + ty;

و ما واقعاً به آنها اهمیت نمی دهیم. این به طرز شگفت انگیزی شبیه کد ترجمه نمونه ترجمه ما است. به همین ترتیب بیایید چرخش را انجام دهیم. همانطور که در پست چرخش اشاره کردیم ما فقط به سینوس و کسینوس زاویه ای که می خواهیم در آن بچرخیم نیاز داریم.

s = Math.sin(angleToRotateInRadians);
c = Math.cos(angleToRotateInRadians);

و ما یک ماتریس مانند این می سازیم

ج	-s	0.0
س	ج	0.0
0.0	0.0	1.0

با اعمال ماتریس این را دریافت می کنیم

newX = x * c + y * s + 1 * 0

newY = x * -s + y * c + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

سیاه کردن همه ضرب در 0 و 1 دریافت می کنیم

newX = x *  c + y * s;
newY = x * -s + y * c;

دقیقا همان چیزی است که ما در نمونه چرخشی خود داشتیم. و در آخر مقیاس. ما 2 عامل مقیاس خود را sx و sy می نامیم و ماتریسی مانند این می سازیم

sx	0.0	0.0
0.0	sy	0.0
0.0	0.0	1.0

با اعمال ماتریس این را دریافت می کنیم

newX = x * sx + y * 0 + 1 * 0

newY = x * 0 + y * sy + 1 * 0

extra = x * 0.0 + y * 0.0 + 1 * 1

که واقعا

newX = x * sx;
newY = y * sy;

که همان نمونه مقیاس بندی ما است. حالا مطمئنم شاید هنوز فکر می کنی. پس چی؟ چه فایده ای دارد. به نظر می رسد کار زیادی برای انجام همان کاری است که قبلا انجام می دادیم؟ اینجاست که جادو وارد می‌شود. معلوم می‌شود که ما می‌توانیم ماتریس‌ها را با هم ضرب کنیم و همه تبدیل‌ها را به یکباره اعمال کنیم. فرض کنید تابع matrixMultiply داریم که دو ماتریس می گیرد، آنها را ضرب می کند و نتیجه را برمی گرداند. برای شفاف‌تر کردن مسائل، اجازه دهید توابعی برای ساخت ماتریس‌هایی برای ترجمه، چرخش و مقیاس بسازیم.

function makeTranslation(tx, ty) {
  return [
    1, 0, 0,
    0, 1, 0,
    tx, ty, 1
  ];
}

function makeRotation(angleInRadians) {
  var c = Math.cos(angleInRadians);
  var s = Math.sin(angleInRadians);
  return [
    c,-s, 0,
    s, c, 0,
    0, 0, 1
  ];
}

function makeScale(sx, sy) {
  return [
    sx, 0, 0,
    0, sy, 0,
    0, 0, 1
  ];
}

حالا بیایید شیدرمان را عوض کنیم. شیدر قدیمی شبیه این بود

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform vec2 u_translation;
uniform vec2 u_rotation;
uniform vec2 u_scale;

void main() {
  // Scale the positon
  vec2 scaledPosition = a_position * u_scale;

  // Rotate the position
  vec2 rotatedPosition = vec2(
     scaledPosition.x * u_rotation.y + scaledPosition.y * u_rotation.x,
     scaledPosition.y * u_rotation.y - scaledPosition.x * u_rotation.x);

  // Add in the translation.
  vec2 position = rotatedPosition + u_translation;
  ...

سایه زن جدید ما بسیار ساده تر خواهد بود.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform vec2 u_resolution;
uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  vec2 position = (u_matrix * vec3(a_position, 1)).xy;
  ...

و در اینجا نحوه استفاده ما از آن است

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix =
       makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

    // Set the matrix.
    gl.uniformMatrix3fv(matrixLocation, false, matrix);

    // Draw the rectangle.
    gl.drawArrays(gl.TRIANGLES, 0, 18);
  }

با این حال، ممکن است بپرسید، پس چه؟ به نظر می رسد که این مزیت چندانی ندارد. اما، حالا اگر بخواهیم ترتیب را تغییر دهیم، مجبور نیستیم یک سایه زن جدید بنویسیم. ما فقط می توانیم ریاضی را تغییر دهیم.

    ...
    // Multiply the matrices.
    var matrix = matrixMultiply(translationMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, scaleMatrix);
    ...

توانایی اعمال ماتریس‌هایی مانند این به‌ویژه برای انیمیشن‌های سلسله مراتبی مانند بازوها روی بدن، ماه‌ها در سیاره اطراف خورشید یا شاخه‌های روی درخت مهم است. برای یک مثال ساده از انیمیشن سلسله مراتبی، اجازه می دهد تا 5 بار "F" خود را بکشیم، اما هر بار اجازه دهید با ماتریس از "F" قبلی شروع کنیم.

  // Draw the scene.
  function drawScene() {
    // Clear the canvas.
    gl.clear(gl.COLOR_BUFFER_BIT);

    // Compute the matrices
    var translationMatrix = makeTranslation(translation[0], translation[1]);
    var rotationMatrix = makeRotation(angleInRadians);
    var scaleMatrix = makeScale(scale[0], scale[1]);

    // Starting Matrix.
    var matrix = makeIdentity();

    for (var i = 0; i < 5; ++i) {
      // Multiply the matrices.
      matrix = matrixMultiply(matrix, scaleMatrix);
      matrix = matrixMultiply(matrix, rotationMatrix);
      matrix = matrixMultiply(matrix, translationMatrix);

      // Set the matrix.
      gl.uniformMatrix3fv(matrixLocation, false, matrix);

      // Draw the geometry.
      gl.drawArrays(gl.TRIANGLES, 0, 18);
    }
  }

برای این کار ما تابع makeIdentity معرفی کردیم که یک ماتریس هویت می سازد. ماتریس هویت ماتریسی است که به طور موثر 1.0 را نشان می دهد به طوری که اگر در هویت ضرب کنید هیچ اتفاقی نمی افتد. درست مثل

X * 1 = X

همینطور

matrixX * identity = matrixX

در اینجا کد ایجاد یک ماتریس هویت است.

function makeIdentity() {
  return [
    1, 0, 0,
    0, 1, 0,
    0, 0, 1
  ];
}

یک مثال دیگر، در هر نمونه ای که تاکنون وجود دارد، "F" ما در گوشه سمت چپ بالای خود می چرخد. دلیلش این است که ریاضیاتی که استفاده می کنیم همیشه حول مبدا می چرخد ​​و گوشه سمت چپ بالای F ما در مبدا است، (0، 0) اما اکنون، چون می توانیم ریاضیات ماتریسی انجام دهیم و می توانیم ترتیب تبدیل را انتخاب کنیم. اعمال می شوند، می توانیم مبدا را قبل از اعمال بقیه تبدیل ها جابجا کنیم.

    // make a matrix that will move the origin of the 'F' to
    // its center.
    var moveOriginMatrix = makeTranslation(-50, -75);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(moveOriginMatrix, scaleMatrix);
    matrix = matrixMultiply(matrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);

با استفاده از آن تکنیک می توانید از هر نقطه بچرخید یا مقیاس کنید. اکنون می دانید که چگونه فتوشاپ یا فلش به شما اجازه می دهند نقطه چرخش را جابجا کنید. بیا دیوانه تر شویم. اگر به اولین مقاله در مورد اصول WebGL برگردید، ممکن است به یاد داشته باشید که ما کدی در سایه زن برای تبدیل از پیکسل به فضای کلیپ داریم که شبیه به این است.

  ...
  // convert the rectangle from pixels to 0.0 to 1.0
  vec2 zeroToOne = position / u_resolution;

  // convert from 0->1 to 0->2
  vec2 zeroToTwo = zeroToOne * 2.0;

  // convert from 0->2 to -1->+1 (clipspace)
  vec2 clipSpace = zeroToTwo - 1.0;

  gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);

اگر به ترتیب به هر یک از این مراحل نگاه کنید، اولین مرحله، "تبدیل از پیکسل به 0.0 به 1.0"، واقعاً یک عملیات مقیاس است. دومی نیز یک عملیات مقیاس است. بعدی یک ترجمه است و آخرین مقیاس Y در -1 است. ما در واقع می توانیم این کار را در ماتریسی که به سایه زن منتقل می کنیم، انجام دهیم. ما می‌توانیم 2 ماتریس مقیاس بسازیم، یکی برای مقیاس 1.0/رزولیشن، دیگری برای مقیاس 2.0، ماتریس سوم برای ترجمه -1.0، -1.0 و چهارم برای مقیاس Y در -1 و سپس همه آنها را با هم ضرب کنیم، اما در عوض، ریاضی ساده است، ما فقط تابعی خواهیم ساخت که مستقیماً یک ماتریس «طرح‌نمایی» برای وضوح مشخص می‌سازد.

function make2DProjection(width, height) {
  // Note: This matrix flips the Y axis so that 0 is at the top.
  return [
    2 / width, 0, 0,
    0, -2 / height, 0,
    -1, 1, 1
  ];
}

اکنون می توانیم سایه زن را حتی بیشتر ساده کنیم. در اینجا کل سایه زن راس جدید است.

<script id="2d-vertex-shader" type="x-shader/x-vertex">
attribute vec2 a_position;

uniform mat3 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
</script>

و در جاوا اسکریپت باید در ماتریس پروجکشن ضرب کنیم

  // Draw the scene.
  function drawScene() {
    ...
    // Compute the matrices
    var projectionMatrix =
       make2DProjection(canvas.width, canvas.height);
    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    ...
  }

ما همچنین کدی را که رزولوشن را تنظیم می کرد حذف کردیم. با این مرحله آخر، ما از یک سایه زن نسبتاً پیچیده با 6-7 مرحله به یک سایه زن بسیار ساده با تنها 1 مرحله تبدیل شده ایم.

امیدوارم این مقاله به ابهام زدایی از ریاضیات ماتریس کمک کرده باشد. در ادامه به سراغ سه بعدی می‌روم. در ماتریس سه بعدی، ریاضیات از همان اصول و کاربرد پیروی می کنند. من با دوبعدی شروع کردم تا بتوانم درک آن را ساده نگه دارم.